Yapay Sinir Ağları Neden Bu Kadar Güçlü?

Yapay Zekanın Sihri: Sinir Ağlarının Gücü

Yapay sinir ağları, günümüz teknolojisinin birçok alanında devrim yaratıyor. Peki, bu sistemler neden bu kadar etkili? 1989 yılında George Cybenko, Yapay Sinir Ağlarının başarısını matematiksel bir temele oturtan bir makale yayımladı ve “Evrensel Yaklaşım Teoremi” adını verdiği bir teoriyle bunu açıkladı.

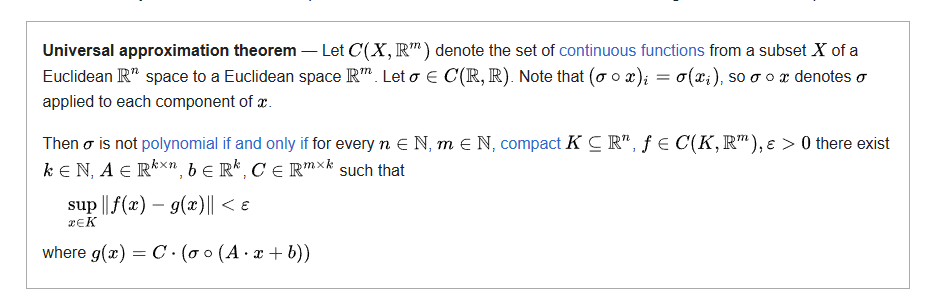
Bu teori, sinir ağlarının doğru şekilde eğitildiğinde karmaşık fonksiyonları taklit edebileceğini gösteriyor. Basitçe söylemek gerekirse, bir yapay sinir ağı, yeterince veriyle eğitildiğinde görüntü tanıma, ses işleme ve hatta dil çevirisi gibi birçok karmaşık problemi çözebilir.

Yapay sinir ağlarının bu kadar etkili olmasının sırrı, işte bu Evrensel Yaklaşım Teoremi’nde saklı! Sinir ağlarının çalışma prensibini anlamak, bu teknolojinin hayatımızı nasıl değiştirdiğini daha iyi kavramamıza yardımcı olabilir.

Şimdi, bu sihrin nasıl işlediğini öğrenmek için bir adım atmaya ne dersiniz?

Yapay Sinir Ağlarının Matematiksel Temeli: Evrensel Yaklaşım Teoremi

Evrensel Yaklaşım Teoremi, [0, 1] aralığında sürekli bir fonksiyon için, belirli bir doğruluk payı içinde bu fonksiyonu yaklaşık olarak modelleyebilecek bir yapay sinir ağı bulunduğunu garanti eder. Ancak dikkat edilmesi gereken bir nokta var: Bu teorem size bu sinir ağını nasıl bulacağınızı söylemez, sadece böyle bir sinir ağının var olduğunu garanti eder. Yine de bu oldukça etkileyici, değil mi?

Bu makalenin devamında, George Cybenko’nun bu teoremi kanıtlarken kullandığı soyut matematiksel yöntemleri (Topoloji ve Fonksiyonel Analiz) açıklayacağım. Görselleştirilmiş bir kanıt yerine, daha derin bir matematiksel anlayış sunmayı amaçlıyorum. Makalenin sonunda, soyut matematiğin gerçek dünya problemlerini çözmekte nasıl kullanıldığını daha iyi kavrayabileceksiniz.

Matematiksel Kanıtın Önemi

Yapay sinir ağlarının neden bu kadar etkili olduğuna dair sezgisel bir anlayışa sahip olmak önemlidir. Ancak bu anlayışı sağlam bir matematiksel temele oturtmak, teknolojiyi geliştirmek ve sınırlarını anlamak açısından kritik bir rol oynar.

Sıradaki bölümde, Evrensel Yaklaşım Teoremi’nin arkasındaki matematiksel yapıyı inceleyerek bu teknolojinin sihrine biraz daha yakından bakacağız!

Fonksiyonel Analiz ve Temel Kavramlar

Evrensel Yaklaşım Teoremi’nin kanıtında C(Im) gibi sürekli fonksiyon uzaylarının bir vektör uzayı olmasından faydalanıyoruz. Ancak bu yalnızca başlangıç; teoremin derinliklerini anlamak için Fonksiyonel Analiz’in daha ileri kavramlarına ihtiyacımız var.

Bu noktada, özellikle topoloji ve norm kavramlarını ele alacağız. Yapay sinir ağlarının sürekli fonksiyonları modelleme yeteneğini anlamak için bu kavramların nasıl bir araya geldiğini keşfetmek önemli.

Sürekli Fonksiyonlar ve Norm Kavramı

Bir fonksiyonun normu, o fonksiyonun büyüklüğünü veya “uzaklığını” ölçer. C(Im) uzayında bir fonksiyonun normu genellikle maksimum değerine göre tanımlanır:

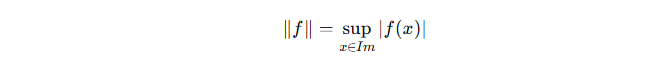
Bu norm, fonksiyonlar arasındaki farkı ölçmek için bir araç sağlar. Örneğin, iki fonksiyon ff ve gg arasındaki fark:

Bu özellik, yapay sinir ağlarının bir fonksiyonu ne kadar iyi modellediğini anlamamızı sağlayan bir metrik olarak kullanılır. Bir sinir ağının tahmini fonksiyonu g(x)g(x), hedef fonksiyon f(x)f(x)’e yakınsa, bu fark küçük bir değere sahip olacaktır.

Yoğunluk Kavramı ve Evrensel Yaklaşım

Evrensel Yaklaşım Teoremi’nin en kritik noktalarından biri yoğunluk kavramıdır. Yoğunluk, bir uzaydaki belirli bir alt kümenin, uzaydaki herhangi bir öğeye istenilen yakınlıkta yaklaşabilme yeteneğini ifade eder. C(Im) uzayında sinir ağlarının temel fonksiyonları bu yoğunluk ilkesine dayanır.

Örneğin, teorem şu şekilde çalışır:

Yapay sinir ağları, aktivasyon fonksiyonlarıyla belirli bir alt uzayı temsil eder.
Bu alt uzay, C(Im)’de yoğun bir kümedir.
Yani, sürekli bir fonksiyon olan f(x), yapay sinir ağlarının bu alt kümesindeki bir fonksiyon olan g(x)’e istediğimiz kadar yakın olabilir.

Bu noktada aktivasyon fonksiyonlarının seçimi, ağın kapasitesini ve temsil yeteneğini doğrudan etkiler. Sigmoid ve ReLU gibi yaygın aktivasyon fonksiyonlarının neden bu kadar etkili olduğunu anlamak için yoğunluk ilkesini ve fonksiyonel analizi daha derinlemesine incelememiz gerekir.

Bir sonraki adımda, bu yoğunluk ilkesinin kanıtına ve yapay sinir ağlarının temel mimarisinin Evrensel Yaklaşım Teoremi ile nasıl ilişkilendiğine odaklanacağız.

C(Im) Bir Normlu Uzaydır

C(Im) yalnızca bir vektör uzayı değil, aynı zamanda bir normlu uzaydır. Bir normlu uzay (V, ∥·∥) şeklinde tanımlanır, burada V, reel veya karmaşık sayılar üzerinde tanımlı bir vektör uzayıdır ve ∥·∥ bir norm fonksiyonu ile tanımlanır. Norm, gerçekte bir vektörün “uzunluğu” veya “büyüklüğü” olarak düşünülebilir. Norm, vektör uzayındaki her öğe için reel değerli bir fonksiyondur: ∥·∥: V → ℝ ve aşağıdaki özelliklere sahiptir:

N1: ∥x∥ ≥ 0 (Norm, her zaman sıfırdan büyük veya sıfırdır.)
N2: ∥x∥ = 0 ⇔ x = 0 (Bir öğenin normu sıfırsa, o öğe sıfırdır.)
N3: ∥αx∥ = |α|∥x∥ (Bir skalerle çarpılan vektörün normu, skalerin mutlak değeri ile vektörün normunun çarpımına eşittir.)
N4: ∥x + y∥ ≤ ∥x∥ + ∥y∥ (Norm, toplama işlemi için üçgen eşitsizliği sağlar.)

Bu özellikleri kullanarak, C(Im) uzayındaki normu tanımlayalım:

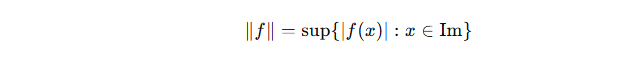
Şimdi, ∥·∥ fonksiyonunun bir norm olduğunu kanıtlayalım.

Kanıt:

fff, g∈C(Im)g \in C(Im)g∈C(Im) olsun.

N1:

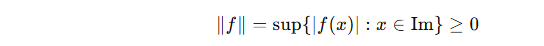
Norm her zaman sıfırdan büyük veya sıfırdır.

N2:

Eğer norm sıfırsa, fonksiyon her noktada sıfırdır.

N3:

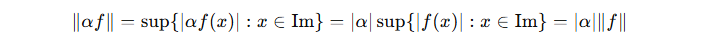
Bir skalerle çarpılan fonksiyonun normu, skalerin mutlak değeri ile fonksiyonun normunun çarpımına eşittir.

N4:

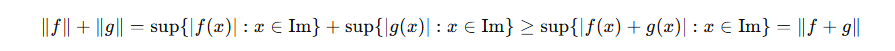
Üçgen eşitsizliğini sağlarız. Bu, fonksiyonlar toplandığında normun, her iki fonksiyonun normlarının toplamından küçük veya eşit olacağını gösterir.

Bu dört özellik, ∥·∥ fonksiyonunun bir norm olduğunu kanıtlar.

C(Im) Bir Metrik Uzay ve Topolojik Uzaydır

Bir vektör uzayı normlu bir uzay olduğunda, bu uzay aynı zamanda bir metrik uzay (Metric Space) ve topolojik uzay (Topological Space) olacaktır.

Bir Metrik Uzay, (M, d) şeklinde sıralanmış bir çift olup, burada M, üzerinde bir metrik d’nin tanımlandığı bir kümedir. Metrik, gerçek dünyada “mesafe” kavramını temsil eden sezgisel bir anlayıştır. Metrik, küme üzerinde tanımlanmış, d: M x M → [0, ∞) fonksiyonu olan, negatif olmayan bir fonksiyondur ve aşağıdaki özelliklere sahiptir:

M1: d(f, g) = 0 ⇔ f = g
M2: d(g, f) = d(f, g)
M3: d(f, g) + d(g, h) ≥ d(f, h)

d(f, g) fonksiyonunu tanımlayalım:
d(f, g): M × M → [0, ∞), burada f, g ∈ M ve M bir normlu uzaydır.
d(f, g) = ||f – g||

Şimdi, d(·, ·)’nin bir metrik olduğunu kanıtlayalım.

Kanıt:
f, g, h ∈ M için:

M1: d(f, g) = 0 ⇔ ||f – g|| = 0 ⇔ f – g = 0 ⇔ f = g

M2: d(g, f) = ||g – f|| = ||(-1)(f – g)|| = |-1| ||f – g|| = d(f, g)

M3: d(f, g) + d(g, h) = ||f – g|| + ||g – h|| ≥ ||f – h|| = d(f, h)

d(·, ·) bir metriktir.

C(Im) bir normlu uzay olduğundan, aynı zamanda bir metrik uzaydır.

M1: d ( f , g ) = 0 ⇔ f = g
M2: d ( g , f ) = d ( f , g )
M3: d ( f , g ) + d ( g , h ) ≥ d ( f , h )

d(f, g) fonksiyonunu tanımlayalım: d ( f , g ) : M × M → [ 0 , ∞ ), burada f , g ∈ M ve M bir normlu uzaydır.
d ( f , g ) = ∥ f – g ∥

Şimdi, d(⋅,⋅)’in bir metrik olduğunu kanıtlayalım.

Kanıt:

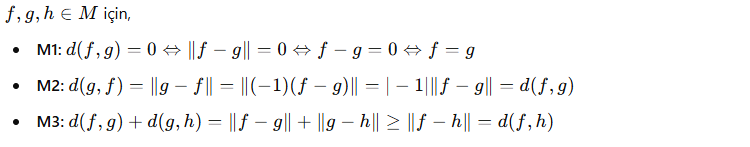
Sonuç olarak,
d(⋅,⋅) bir metriktir.

C(Im) bir normlu uzay olduğundan, aynı zamanda bir metrik uzaydır.

Bir Topolojik Uzay, (X, τ) sıralı bir ikilidir, burada X bir küme ve τ, X kümesinin açık kümelerinden oluşan bir koleksiyondur ve şu aksiyomları sağlar:

T1: ∅, X ∈ τ
T2: τ kümesindeki kümelerin (sonlu veya sonsuz) her bir birleşimi yine τ kümesindendir, yani ∪ui ∈ τ her ui ∈ τ için
T3: τ kümesindeki kümelerin her sonlu kesişimi yine τ kümesindendir, yani ∩ui ∈ τ her ui ∈ τ için

Bir Metrik Uzay (M, d)’nin aynı zamanda Topolojik Bir Uzay olduğunu anlamak için Open Ball (Açık Top) adlı bir araç kullanmamız gerekiyor:

Açık Top B(x, r) Tanımla
B(x, r) her x ∈ M, r > 0 için
B(x, r) = {p | p ∈ M, d(x, p) < r}

Açık Küme o ve koleksiyon τ’yu Tanımla
τ = {o | o ⊆ M, ∀ x ∈ o ∃ r > 0 (B(x, r) ⊆ o)}

Şimdi, (M, d)’nin bir Topolojik Uzay olduğunu kanıtlayalım.

Kanıt

T1:
∅, hiçbir nokta içermez ⇒ ∅ ∈ τ
∀x ∈ M ∃ r > 0 B(x, r) ⊆ M ⇒ M ∈ τ
T2:
o[i] ∈ τ
⇒ ∪o[i] ⊆ M
∪o[i] = {x | ∃o ∈ τ ∃ r > 0 (x ∈ o ve B(x, r) ⊆ o ⊆ ∪o[i])}
⇒ ∪o[i] ⊆ M
∪o[i] = {x | ∃ r > 0 (B(x, r) ⊆ ∪o[i])}
⇒ ∪o[i] ∈ τ
T3:
o1, o2 ∈ τ
⇒ o1 ∩ o2 ⊆ M
o1 ∩ o2 = {x | ∃ r1 > 0 ∃ r2 > 0 (x ∈ o1 ve B(x, r1) ⊆ o1 ve x ∈ o2 ve B(x, r2) ⊆ o2)}
⇒ o1 ∩ o2 ⊆ M
o1 ∩ o2 = {x | ∃ min(r1, r2) > 0 (x ∈ o1 ∩ o2 ve B(x, min(r1, r2)) ⊆ B(x, r1) ⊆ o1 ve B(x, min(r1, r2)) ⊆ B(x, r2) ⊆ o2)}
⇒ o1 ∩ o2 ⊆ M
o1 ∩ o2 = {x | ∃ min(r1, r2) > 0 (B(x, min(r1, r2)) ⊆ o1 ∩ o2)}
⇒ o1 ∩ o2 ∈ τ

(M,d) bir Topolojik Uzaydır.

F(x) biçimindeki fonksiyonlar C(Im) içinde yoğundur mu?

Evrensel Yaklaşım Teoremi’ne geri dönersek, “F(x) biçimindeki fonksiyonlar C(Im) içinde yoğundur” der. S, F(x) biçimindeki fonksiyonların kümesidir. Açıkça, S kümesi C(Im) kümesinin bir alt kümesidir. Yoğunluk, topolojik bir özelliktir. Bu, C(Im) içindeki herhangi bir x noktası için, x’in her komşuluğu N’nin, S kümesinden bir noktayı içerdiği anlamına gelir. x’in bir komşuluğu N, C(Im) kümesinin x’i içeren bir açık küme u’yu içeren bir alt kümesidir.

x ∈ u ⊆ N

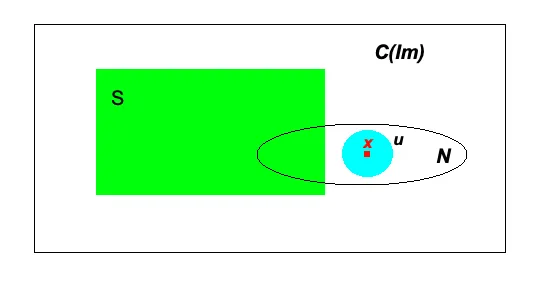
Metrik Uzayında, her Açık Topun aynı zamanda bir Açık Küme ve komşuluk olabileceği kanıtlanabilir [Bkz. Ek]:

x∈B(x, r) = u = N

C(Im)’in bir Topolojik Uzay olduğunu kanıtladık, bu nedenle artık Topoloji Teorisi’ni kullanarak teoremi kanıtlamamıza yardımcı olabiliriz. Şimdi, Evrensel Yaklaşım Teoremi’ni Topoloji Teorisi dilinde ifade edebiliriz:

S, C(Im) içinde yoğundur
⇔ Herhangi bir f ∈ C(Im) için, N ∩ S ≠ ∅ ∀ N, burada N f’nin bir komşuluğudur
⇒ Herhangi bir f ∈ C(Im) için, B(f, ε) ∩ S ≠ ∅ ∀ε > 0
⇒ Herhangi bir f ∈ C(Im) için, ∀ε > 0, ∃ F ∈ S öyle ki d(f, F) < ε
⇒ Herhangi bir f ∈ C(Im) için, ∀ε > 0, ∃ F ∈ S öyle ki ∥f – F∥ < ε
⇒ Herhangi bir f ∈ C(Im) için, ∀ε > 0, ∃ F ∈ S öyle ki sup{|F(x) – f(x)| ∀ x ∈ Im} < ε
⇒ Herhangi bir f ∈ C(Im) için, ∀ε > 0, ∃ F ∈ S öyle ki |F(x) – f(x)| < ε ∀ x ∈ Im

Böylece, S’nin C(Im) içinde yoğun olduğunu kanıtladıktan sonra, Evrensel Yaklaşım Teoremi nihayet kanıtlanmış olur. Bunu kanıtlamak için aşağıdaki Topoloji teoremini kullanarak ve sonra çelişki yoluyla kanıtlayacağız:

S, C(Im) içinde yoğundur ⇔ Kapanış(S) = C(Im)
Kapanış(S) ≠ C(Im) olduğunu varsayalım ⇒ Kapanış(S) ⊂ C(Im) ⇒ çelişki

Evrensel Yaklaşım Teoremi ve Yapay Sinir Ağları

Bu makalede Evrensel Yaklaşım Teoremi’ni tanıtıyoruz. Bu teorem, Yapay Sinir Ağları’nın nasıl çalıştığını açıklayan önemli bir matematiksel kavramdır.

C(Im), reel değerli sürekli fonksiyonlar kümesidir ve hem normlu bir vektör uzayı hem de topolojik bir uzaydır. Evrensel Yaklaşım Teoremi, S kümesinin C(Im) içinde yoğun olduğunu göstererek kanıtlanır.

Bu teoremi kanıtlamak için, S kümesinin kapanışının C(Im) ile aynı olması gerektiği ispatlanır. Detaylı kanıtlar 2. bölümde ele alınacaktır.

Topoloji hakkında daha fazla bilgi için makale serimi takip edebilirsiniz.

Arif GÖKÇE